Contenido de examenes

PRIMERO BASICO

operaciones con fracciones
porcentaje
proposiciones
figuras geometricas
estadistica

SEGUNDO BASICO

Proposiciones
ecuaciones
figuras geometricas

TERCERO BASICO MATEMATICAS

ecuaciones cuadraticas
ecuaciones lineales
numeracion maya
numeracion binaria
ecuaciones con radicales

TERCERO BASICO FISICA

mru
mruv
caida libre
tiro vertical

CUARTO BACHILLERATO

MATEMATICAS

Ecuaciones cuadraticas
ecuaciones lineales
desgualdades lineales
desigualdades cuadraticas

FISICA

mru
mruv

LOGICA

proposiciones
conectivos logicos
conectivos existenciales

PSICOLOGIA

motivacion
necesidades
liderazgo
autoridad
poder

QUINTO BACHILLERATO

MATEMATICAS
sistema maya
sistema binario
proposiciones
ecuaciones cuadraticas
fracciones

ESTADISTICA

limites inferiores y superiores
frecuencia
frecuencia acumulada
frecuencia porcentual
grafica de barras
grafica de pastel

QUIMICA

tabla periodica

tarea de matematicas 4to bach

1

2

3

4

5

6

7

8

9

10

Excelente

La historia de un Guatemalteco ejemplar... http://servicios.prensalibre.com/pl/domingo/archivo/revistad/2005/noviembre05/271105/dfrente.shtml

grafica de su calificacion

Link para test del coeficiente intelectual

http://www.psicoactiva.com/tests/testci.htm

trabajo de 4to bach

Resolver los siguientes problemas:

Problema n° 1) ¿A cuántos m/s equivale la velocidad de un móvil que se desplaza a 72 km/h?

Problema n° 2) Un móvil viaja en línea recta con una velocidad media de 1.200 cm/s durante 9 s, y luego con velocidad media de 480 cm/s durante 7 s, siendo ambas velocidades del mismo sentido:

a) ¿cuál es el desplazamiento total en el viaje de 16 s?.

b) ¿cuál es la velocidad media del viaje completo?.

Problema n° 3) Resolver el problema anterior, suponiendo que las velocidades son de distinto sentido.

Se lanza verticalmente hacia arriba una pelota con una velocidad inicial de 30 m/s,calcula:
a)Tiempo que tarda en alcanzar su altura max.
b)Altura max.
c) Posición y velocidad de la pelota a los 2s de haberse lanzado

 Se lanza una piedra verticalmente hacia arriba, con una velocidad inicial de 58,8m/s. Halla:
a) Posición que ocupa al cabo de 2 s.
b) Velocidad de la piedra al cabo de 2 s.
c) La altura máxima que alcanza y el tiempo empleado.

Se lanza una piedra verticalmente hacia arriba, con una velocidad inicial de 39,2 m/s. Halla:
a) El tiempo que tarda en llegar al punto más alto.
b) La altura máxima que alcanza.
c) El tiempo que tarda en alcanzar la altura de 50 m. 
d) La velocidad que lleva a los 50 m de altura.

 Se deja caer una pelota desde la parte alta de un edificio, si tarda 3s en llegar al piso ¿Cuál es la altura del edificio? ¿Con qué velocidad se impacta contra el piso?

Se deja caer una pelota desde una altura de 20 m.
a) ¿Cuánto tarda en llegar al suelo?
b) ¿Con qué velocidad llega?.

Se patea un balón de fútbol con un ángulo de 37° con una velocidad de 20 m/s. Calcule:

a) La altura máxima.

b) El tiempo que permanece en el aire.

c) La distancia a la que llega al suelo.

d) La velocidad en X y Y del proyectil después de 1 seg de haber sido disparado

1.- Un proyectil es disparado con una rapidez inicial de 75.2 mIs, a un ángulo de 34.5° por encima de la horizontal a lo largo de un campo de tiro plano. Calcule

a) La máxima altura alcanzada por el proyectil.

b) El tiempo que total que el proyectil permanece en el aire

c) La distancia horizontal total

d) La velocidad de X y Y del proyectil después de 1.5 s de haber sido disparado

2.- Una flecha se dispara con un ángulo de 50° con respecto a la horizontal y con una velocidad de 35 m/s.

a) ¿Cuál es su posición horizontal y vertical después de 4 segundos?

b) Determine las componentes de su velocidad después de 4 segundos.

c) ¿Cuál es la velocidad en X y Y después de 4 segundos?

ahi les dejo los problemas espero que los puedan resolver son para el dia miercoles 2 de agosto feliz dia

pruebas liberadas

http://www.mineduc.gob.gt/DIGEDUCA/documents/pruebasLiberadas/graduandos/PL-Mate-Grad2010.pdf



http://www.mineduc.gob.gt/DIGEDUCA/documents/pruebasLiberadas/graduandos/2009_graduandos_matematicas.pdf

aca les dejo los examenes  resueltos porfavor revisarlos y hacer la tarea

feria de la ciencia

Muybien jovenes ahi esta la informacion de la feria recuerden el informe debe contener:
- 5 empresas participantes
- comentario de lo que piensan de la feria
- producto que les llamo la atencion
- 5 volantes diferentes y una foto de asistencia a el evento

Repaso de ecuaciones cuadraticas

Ecuaciones de segundo grado (o cuadráticas)

Ecuaciones de segundo grado y una incógnita

Sabemos que una ecuación es una relación matemática entre números y letras. Normalmente se trabaja con ecuaciones en las que sólo hay una letra, llamada incógnita, que suele ser la x.

Resolver la ecuación consiste en encontrar un valor (o varios) que, al sustituirlo por la incógnita, haga que sea cierta la igualdad.

Ese valor es la solución de la ecuación.

Ejemplo: Resolver la ecuación    x − 1 = 0

El número que hace que esa ecuación sea cierta es el 1, ya que 1 – 1 = 0, por lo tanto, 1 es la solución de la ecuación.

Si en la ecuación la incógnita está elevada al cuadrado, decimos que es una ecuación de segundo grado (llamadas también ecuaciones cuadráticas), que se caracterizan porque pueden tener dos soluciones (aunque también una sola, e incluso ninguna).

Cualquier ecuación de segundo grado o cuadrática se puede expresar de la siguiente forma:

                                 ax² + bx + c = 0

Donde a, b y c son unos parámetros que habrá que sustituir por los números reales que corresponda en cada caso particular.

Solución de ecuaciones cuadráticas

Hemos visto que una ecuación cuadrática es una ecuación en su forma ax² + bx + c = 0, donde  a, b, y c son números reales.
 
Pero este tipo de ecuación puede presentarse de diferentes formas:

Ejemplos:

9x² + 6x + 10 = 0        a = 9, b = 6, c = 10

3x²  – 9x  + 0  = 0        a = 3, b = –9, c = 0  (el cero, la c, no se escribe, no está)

–6x² + 0x + 10 = 0       a = -6, b = 0, c = 10 (el cero equis, la b, no se escribe)

Para resolver la ecuación cuadrática de la forma ax² + bx + c = 0 (o cualquiera de las formas mostradas), puede usarse cualquiera de los siguientes métodos: 
 
Solución por factorización

En toda ecuación  cuadrática uno  de sus miembros es un polinomio de segundo grado y el otro es cero; entonces, cuando el polinomio de segundo grado pueda factorizarse, tenemos que convertirlo en un producto de binomios.

Obtenido el producto de binomios, debemos buscar el valor de x de cada uno.

Para hacerlo igualamos a cero cada factor y se despeja para la variable. Igualamos a cero ya que sabemos que si un producto es igual a cero, uno de sus multiplicandos, o ambos, es igual a cero.

Ejemplos

1) Resolver

(x + 3)(2x − 1) = 9

Lo primero es igualar la ecuación a cero.

Para hacerlo, multiplicamos los binomios:

Ahora, pasamos el 9, con signo contrario, al primer miembro para igualar a cero:

Ahora podemos factorizar esta ecuación:

(2x − 3)(x + 4) = 0

Ahora podemos igualar a cero cada término del producto para resolver las incógnitas:

Si

2x − 3 = 0

2x = 3

Si

x + 4 = 0

x = −4

Esta misma ecuación pudo haberse presentado de varias formas:

(x + 3)(2x − 1) = 9

2x² + 5x − 12 = 0

2x² + 5x = 12

2x² − 12 = − 5x

En todos los casos la solución por factorización es la misma:

2) Halle las soluciones de

La ecuación ya está igualada a cero y solo hay que factorizar e igualar sus factores a cero y luego resolver en términos de x:

Ahora, si

x = 0

o si

x− 4 = 0

x = 4

Algunos ejercicios: Resolver cada ecuación por el método de factorización:

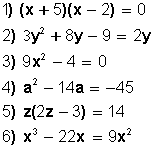
Soluciones:

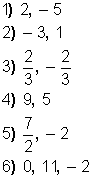
Solución por completación de cuadrados

Se llama método de la completación de cuadrados porque se puede completar un cuadrado geométricamente, y porque en la ecuación cuadrática se pueden realizar operaciones algebraicas que la transforman en una ecuación del tipo:

(ax + b)² = n

en la cual el primer miembro de la ecuación (ax + b)², es el cuadrado de la suma de un binomio.

Partiendo de una ecuación del tipo

x² + bx + c = 0

por ejemplo, la ecuación

x² + 8x = 48, que también puede escribirse   x² + 8x − 48 = 0

Al primer miembro de la ecuación (x² + 8x) le falta un término para completar el cuadrado de la suma de un binomio del tipo
(ax + b)²

Que es lo mismo que

(ax + b) (ax + b)

Que es lo mismo que

ax² + 2axb + b²

En nuestro ejemplo

x² + 8x = 48, el 8 representa al doble del segundo número del binomio, por lo tanto, ese número debe ser obligadamente 8 dividido por 2 (8/2), que es igual a 4, y como en el cuadrado de la suma de un binomio ( a² + 2ab + b²) el tercer término corresponde al cuadrado del segundo término (4² = 16) amplificamos ambos miembros de la ecuación por 16, así tenemos

x² + 8x + 16 = 48 + 16

x² + 8x + 16 = 64

la cual, factorizando, podemos escribir como sigue:

(x + 4) (x + 4) = 64

Que es igual a

(x + 4)² = 64

Extraemos raíz cuadrada de ambos miembros y tenemos

 Nos queda

x + 4 = 8

Entonces

x = 8 − 4

x = 4

Se dice que "se completó un cuadrado" porque para el primer miembro de la ecuación se logró obtener la expresión (x + 4)², que es el cuadrado perfecto de un binomio.

Veamos otro ejemplo:

Partamos con la ecuación

x² + 6x − 16 = 0

Hacemos

x² + 6x = 16

Luego, a partir de la expresión x² + 6x (primer miembro de la ecuación) debemos obtener una expresión de la forma (ax + b)² (cuadrado de la suma de un binomio).

Para encontrar el término que falta hacemos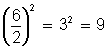 
(Para encontrar dicho término en cualquier ecuación siempre debemos dividir por  2 el valor real del segundo término y el resultado elevarlo al cuadrado).

Ahora, para obtener la expresión completa se suma 9 a ambos miembros de la ecuación:

x² + 6x = 16

x² + 6x + 9 = 16 + 9

x² + 6x  + 9 = 25

factorizamos, y queda

(x +3) (x + 3) = 25

(x + 3)² = 25

La expresión x² + 6x se ha completado para formar un cuadrado perfecto, en este caso (x + 3)², y así la ecuación se resuelve con facilidad:

Extraemos raíz cuadrada

, y queda

x + 3 = 5   y  x + 3 = −5

(pues  5² = 5  y también (−5)² = 5

Entonces

x = 5 − 3 

x = 2

Y

x = − 5 − 3

x = − 8

 La  ecuación 1 da  x = 2   y la ecuación 2 da  x = −8.

Otro  ejemplo para analizar y estudiar:

Resolver la ecuación: x² – 6x + 8 = 0

Veamos: Con los términos x² y –6x podemos formar el cuadrado de binomio (x – 3)² , pero nos faltaría el término igual a 9, por lo tanto, dejamos las equis (x) a la izquierda y pasamos el 8 a la derecha de la igualdad:

x² – 6x = − 8 
y sumamos 9 a ambos lados de la igualdad para que a la izquierda se forme el cuadrado de binomio:

¿Cómo encontramos el término que falta?, haciendo

x² – 6x = −8       /+9 (sumamos 9 en ambos miembros de la ecuación)

x² − 6x + 9 = − 8 + 9

(x – 3)² = 1

Extraemos las raíces cuadradas

y queda

x – 3 = 1    y   x − 3 = −1

Si

x – 3 = 1

x = 1 + 3

x = 4

Si

 x – 3 = −1

x = −1 + 3

x = 2

Por lo tanto  x₁ = 4 y  x₂ = 2

Debemos hacer notar que el método de completar cuadrados terminará en lo mismo que la fórmula general, porque es de este método de donde sale dicha fórmula, usada en el método que vemos a continuación.

Ver: PSU: Matematica; Pregunta 028_2010

Solución por la fórmula general
 
Existe una fórmula que permite resolver cualquier ecuación de segundo grado, que es la siguiente:

La fórmula genera dos respuestas: Una con el signo más (+) y otra con el signo menos (−)  antes de la raíz. Solucionar una ecuación de segundo grado se limita, entonces, a identificar las letras a, b y  c y sustituir sus valores en la fórmula.

La fórmula general para resolver una ecuación de segundo grado sirve para resolver cualquier ecuación de segundo grado, seacompleta o incompleta, y obtener buenos resultados tiene que ver con las técnicas de factorización.

Ejemplo:  

Resolver la ecuación  2x² + 3x − 5 = 0

Vemos claramente que a = 2,     b = 3   y     c = −5, así es que:

Ahora, tenemos que obtener las dos soluciones, con el + y con el − :

  y también      

Así es que las soluciones son .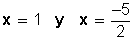

Aquí debemos anotar algo muy importante:

En la fórmula para resolver las ecuaciones de segundo grado aparece la expresión 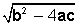. Esa raíz cuadrada sólo existirá cuando el radicando (b² − 4ac) sea positivo o cero.

El radicando b² – 4ac se denomina discriminante y se simboliza por Δ. El número de soluciones (llamadas también raíces)depende del signo de Δ y se puede determinar incluso antes de resolver la ecuación.

Entonces, estudiando el signo del discriminante (una vez resuelto), podemos saber el número de soluciones que posee:

Si Δ es positivo, la ecuación tiene dos soluciones.

Si Δ es negativo, la ecuación no tiene solución.

Si Δ es cero, la ecuación tiene una única solución.

En el ejemplo anterior el discriminante era Δ = 49, positivo, por eso la ecuación tenía dos soluciones.

Obtendremos dos soluciones, una cuando sumamos a − b la raíz y lo dividimos por 2a, y otra solución cuando restamos a − b la raíz y lo dividimos por 2a.

Trabajando con ecuaciones de segundo grado

Como lo dijimos al comienzo, cualquier ecuación de segundo grado puede, mediante transformaciones, expresarse en la forma ax² + bx + c = 0,  donde  a,  y  b  son los coeficientes de los términos  x²  y  x, respectivamente y  c es el término independiente.

Ecuación de segundo grado completa
 
Una ecuación de segundo grado es completa cuando los tres coeficientes  a,  b,  y  c  son distintos de cero.

Entonces, la expresión de una ecuación de segundo grado completa es 

 ax² + bx + c = 0.

Ecuación de segundo grado incompleta

Una ecuación de segundo grado es incompleta cuando los términos  b  o  c,  o ambos, son cero.

(Si a = 0, la ecuación resultante sería  bx + c = 0,  que no es una ecuación de segundo grado.)

La expresión de una ecuación de segundo grado incompleta es:

ax² = 0;   si    b = 0    y    c = 0.

ax² + bx = 0;    si    c = 0.

ax² + c = 0;    si    b = 0.

Algunos ejemplos, con soluciones

1) Resolver: − 5x² + 13x + 6 = 0

Se identifican las letras, cuidando que la ecuación esté ordenada respecto a la x, de grado mayor a menor. Con esta condición tenemos: a = − 5;  b = 13;  c = 6.

Se aplica la fórmula:

Como la raíz buscada es 17 (el cuadrado de 17 es 289), se tiene entonces que:

Según esto, tendremos dos raíces diferentes, una usando el signo + y otra usando el signo −.

Llamaremos X₁ y X₂  a las dos soluciones, que serán:

Ambos valores de x satisfacen la ecuación, es decir, al sustituirlos en ella producen una identidad. Al procedimiento de sustituir para probar si los valores hallados satisfacen la ecuación se le denomina verficación.

Probando con x = 3. Resulta: −5 • (3)2 + 13 • (3) + 6 = −45 + 39 + 6 = 0, tal como se esperaba en el segundo miembro.
Probando con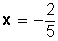 ,  se tiene

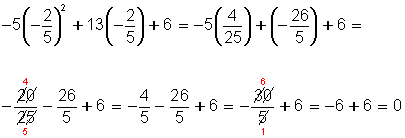
Como ambas respuestas producen identidades, ahora es seguro que 3 y  son las raíces de − 5x² + 13x + 6 = 0

2.- Resolver: 6x − x² = 9

Hacemos los cambios necesarios para que la ecuación tenga la forma conocida. Trasponiendo y cambiando de lugar resulta:

− x² + 6x − 9 = 0. Ahora se identifican las letras:

a = −1 ;  b = 6 ;  c = −9 ; y se aplica la fórmula:

El discriminante (Δ)  es igual a cero, por lo cual se producen dos raíces iguales a 3, es decir, x₁ = x₂ = 3.

Sustituyendo los valores en la ecuación original, se verifica que: 6•3 − 32 = 18 − 9 = 9 con lo cual se ha comprobado la respuesta.

Ejercicios que se resuelven con ecuaciones cuadráticas

En los siguientes ejercicios mostraremos algunos planteamientos que pueden expresarse como una ecuación de segundo grado.

Para hacerlo, hay que entender la lógica del problema, identificando como x a una de las variables que el problema establece; luego deben escribirse las relaciones entre la variable, de acuerdo al planteamiento y, finalmente, se resuelve la ecuación.

Hay que destacar que sólo la experiencia mejora los resultados. Para practicar, los interesados pueden consultar el "Algebra" de Aurelio Baldor, que, para muchos, es la biblia del álgebra.

Problema 1

La suma de dos números es 10 y la suma de sus cuadrados es 58. Halle ambos números

Primero se asigna la variable x a una de las incógnitas del problema. Hay dos incógnitas que son ambos números, como el problema no hace distinción entre uno y otro, puede asignarse x a cualquiera de los dos, por ejemplo:

x = Primer número

Como la suma de ambos es 10, entonces necesariamente el otro será:

10 − x = Segundo número

Para entenderlo mejor:

Si entre su amigo y usted tienen $ 1.000, y su amigo tiene $ 400, ¿Cuánto tiene usted?, obviamente, restando el total menos 400, es decir 1.000 − 400 = $ 600. Si su amigo tiene $ x, la cuenta no cambia, sólo que no sabrá el valor sino en función de x, es decir, usted tiene 1.000 − x .

La condición final del problema establece que la suma de los cuadrados de ambos números resulta 58, entonces:

x² + (10 - x)² = 58

Esta es la ecuación a resolver

Para hacerlo, aplicamos algunas técnicas de álgebra elemental y luego reordenamos para llegar a la fórmula conocida.

Vemos que la operación indicada entre paréntesis es el cuadrado de un binomio. Es un error muy común que los estudiantes escriban: (a − b)² = a² − b²,  lo cual es incorrecto. La expresión correcta es: (a − b)² = a² − 2•a•b + b²

Desarrollando la ecuación se tiene: x² + 10² − 2•10•x + x² = 58 = x² + 100 − 20•x + x² = 58

Ordenando y agrupando: 2x² − 20•x+ 42 = 0;

Dividiendo entre 2 toda la ecuación:

 x² − 10x + 21 = 0

Ahora podemos aplicar la fórmula general para resolver la ecuación de segundo grado y llegaremos a x₁ = 7 y x₂ = 3.

Veamos, si tenemos

a = 1,                b = −10        c = 21

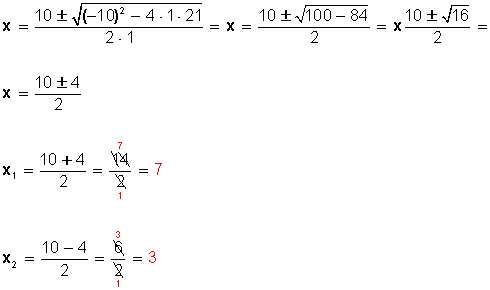
Los números buscados son 7 y 3.

Problema 2

El largo de una sala rectangular es 3 metros mayor que el ancho. Si el ancho aumenta 3 m y el largo aumenta 2 m, el área se duplica. Halle el área original de la sala.

Largo y ancho son diferentes. El problema permite que la variable x se asigne a cualquiera de las dos incógnitas, largo o ancho.

Supongamos que:

x = ancho de la sala

El largo es 3 metros mayor que el ancho, así es que:

x + 3 = largo de la sala.

El área de un rectángulo es la multiplicación de ambos:

x • (x + 3 ) = área de la sala.

Téngase en cuenta que estos son los datos iniciales.

Las condiciones del problema explican que el ancho aumenta en 3 metros y el largo aumenta en 2 metros, así que, luego del aumento quedan:

x + 3 = nuevo ancho de la sala

x + 5 = nuevo largo de la sala

(x + 3 ) • (x + 5) = nueva área de la sala

Según los datos del problema, el área se ha duplicado, así es que planteamos la ecuación:

(x + 3 ) • (x + 5) = 2 • x • (x + 3)

Se efectúan las multiplicaciones: x² + 5x + 3x + 15 = 2x² + 6x

Se pasa todo al primer miembro: x² + 5x + 3x + 15 − 2x² − 6x = 0

Se simplifica: − x2 + 2x + 15 = 0 Esta es la ecuación a resolver.

Se aplica la fórmula conocida y resulta: x₁ = 5 y x₂ = −3.

La solución x = −3 se desecha, ya que x es el ancho de la sala y no puede ser negativo. Se toma como única respuesta que el ancho original (x) era 5 metros.

Como el largo inicial  x + 3 = 8 metros, el área original era 8m • 5m = 40 m².

Problema 3

Halle el área y perímetro del triángulorectángulo mostrado. Las dimensiones están en metros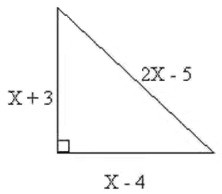 

Como es un triángulo rectángulo se cumple el Teorema de Pitágoras: "El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos" (c² = a² + b²). La hipotenusa es el lado mayor (2x − 5) y los otros dos son los catetos, se plantea entonces la ecuación:

(x + 3)² + (x − 4)² = (2x − 5)²

Desarrollando cada binomio al cuadrado, se tiene:

x² + 2 • 3 • x + 3² + x² − 2 • 4 • x + 4² = (2x)² − 2 • (2x) • 5 + 5² = x² + 6x + 9 + x² − 8x + 16 = 4x² − 20x + 25

Reagrupando:

x² + 6x + 9 + x² − 8x + 16 − 4x² + 20x − 25 = 0

Finalmente:

−2x² + 18x = 0

Es la ecuación a resolver

Las raíces de la ecuación son x₁ = 0 y x₂ = 9.

La solución x = 0 se desecha, ya que entonces un cateto sería −4 m, lo cual no es posible. La solución es entonces, x = 9. De esta manera, el triángulo queda con catetos 12 metros y 5 metros y con hipotenusa 13 metros.

El área de un triángulo es base por altura dividido 2; la base y la altura son los dos catetos que están a 90° , por lo tanto el área es

El perímetro es la suma de los lados, es decir, P = 12 m + 5 m + 13 m = 30 m.

Sentimientos...

Incríble léanlo ... 
Davkett
Sabiendo que iba a ser sacrificado en un matadero, un toro en Hong Kong hizo lo que muchas personas no han podido comprender o son esepticos acerca de lo que se dice de los animales....el mostró tener sentimientos.

Como se reportó en el "Weekly World News", un grupo de trabajadores llevaban al toro a una fábrica empacadora, ellos estaban a punto de matarlos para hacer con el bistecs cuando estaban cerca a la puerta principal del matadero el toro muy afligido de repente se detuvo y no quiso caminar más, se hizo hacia atrás y de pronto cayó de rodillas: el toro estaba llorando.
¿Cómo supo que iba a ser matado desde antes de entrar al matadero? Él es más inteligente que las personas.

El Sr. Shiu, un carnicero recordó, "Cuando yo vi a este supuesto "estúpido" animal sollozando y con sus ojos llenos de temor y lamentación, comencé a temblar, llamé al resto para que vieran lo que sucedía. Ellos estaban tan sorprendidos como yo, continuamos tratando de empujar al toro hacia adelante, pero simplemente no quiso moverse y se quedo ahí sentado, llorando".
Billy Fong, dueño de la empacadora dijo, "La gente cree que los animales no lloran como los seres humanos. Sin embargo ese toro realmente sollozaba como un bebé". En ese momento más de diez hombres fuertes atestiguaron la escena y fueron conmovidos. Aquellos que son los responsables de matarlos con sus propias manos se sintieron mayormente conmovidos y lloraron junto con él.
Otros trabajadores que laboraban en el mismo matadero también se acercaron a ver como lloraba el toro, el cual estaba completamente rodeado de personas, todos estaban en shock mirando la escena. Tres de ellos dijeron que nunca iban a olvidar a ese toro llorando mientras mataban a otros animales.
Con ambos llorando, tanto hombres como el toro, todos sabían que nadie podría matar a ese toro.

El problema era ¿que iban a hacer con el? al final, todos juntaron fondos suficientes para comprarlo y mandarlo a un templo, en donde los amables monjes cuidarían de el de por vida.
Después de que los trabajadores tomaron esta decisión, un milagro sucedió. Un empleado dijo, "Cuando le prometimos al toro que no lo matarían, el comenzó a moverse y nos siguió".

¿Cómo comprendió las palabras de las personas?
Mr. Shiu dijo "Créanlo o no, esto es real, aunque suene increíble". "No hay ninguna duda de que este toro cambio la vida de todos esos carniceros que presenciaron la escena tan impactante".
Esperamos que esta historia, haya cambiado también la tuya"

Dedicado a mis alumnos

Contenido de 5to bach

quimica

tabla periodica con todas sus caracteristicas
elementos

Estadistica

graficas de barras
graficas de pastel
cuadros de distribucion

Matematicas

suma, resta, multiplicacion y division de fracciones algebnraicas
ecuaciones de primer grado

contenido 4to bach

matematicas:
suma, rsta, multiplicacion y division de fracciones algebraicas

fisica
movivmiento rectilineo uniformemente variado
caida libre

Psicologia
psicologia
sociologia
antropologia
ciencia politica
estructura organizacional
principios de una empresa
normas ISO
reingenieria

Logica Matematica
conectivos existenciales
conectivos universales
problemas aplicados de logica

Contenido 3ro basico Fisica

NIveles de organizacion bioticos
ogganizacion abiotica
tejidos
partes de la planta
ciclos biogemicos
ecosistemas
ecosistemas artificiales
evolucion
energia

Contenido de 3ro basico matematicas

simplificacion de fracciones usando todos los casos de factorizacion
suma de fracciones
restas de fracciones
multiplicacion de fracciones
division de fracciones
teorema de extremos y medios

contenido de segundo basico

ecuacion de la recta
angulos
figuras geometricas
volumenes
triangulo rectangulo
teorema de pitagoras

Contenido de primero basico

proposiciones simples
proposciones compuestas
tablas de verdad de la disyuncion, conjuncion, condicional
union e interseccion de conjuntos
conjunots finitos e infinitos
operaciones combinadas de suma resta multiplicacion y division

Algebra de Baldor

Bueno jovenes aqui les dejo el link para el libro de algebra de baldor

http://es.scribd.com/doc/3468883/ALGEBRA-de-BALDOR

hello word...

Guias de estudio para año 2013

Jovenes ahi les dejo las guias de estudio para los examenes de conocimientos basicos...

lenguaje: http://nuevos.usac.edu.gt/guias/lenguaje2012.pdf
mateamtica: http://nuevos.usac.edu.gt/guias/mate2012.pdf
fisica: http://nuevos.usac.edu.gt/guias/fisica2012.pdf
biologia: http://nuevos.usac.edu.gt/guias/biologia2012.pdf
quimica: http://nuevos.usac.edu.gt/guias/quimica2012.pdf